Any coherent analytic category is spatial (4.2.2) and perfect (4.1.2.b). Thus a locally disjunctable coherent analytic category is a spatial analytic geometry, which is simply called a coherent analytic geometry. 

In the following we assume A is a coherent analytic geometry. Recall that (3.6.9) if X is an object. an open subset U of Spec(X) is affine open if it is determined by an analytic subobject of X. The set of affine open subsets is  a base for the topology on Spec(X). 

Proposition 5.1.1. (a) Spec(X) is a coherent space for any object X. 
(b} For any map f: Y --> X the continuous mapping Spec(f): Spec(Y) --> Spec(X) is a mapping of coherent spaces. 

Proof. (a) Suppose {V_i} is a set of disjunctable strong subobjects such that {(V_i)^c | iI}  is an analytic cover for X. Let V be the intersection of these {V_i}. Then by (3.1.10) we have X = 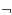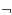{(V_i)^c} = 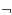V, so V = 0. Since 0 is finitely copresentable by (4.3.2.c), there is a finite subset J  I such that {V_i} | iI} has intersection 0. Applying (3.1.10) again we see that {(V_i)^c} is a finite analytic cover for X. This shows that Spec(X) is quasi-compact. Thus any affine open subset is also quasi-compact. Since affine open subsets form a base for Spec(X), any finite intersection of quasi-compact open subsets is quasi-compact. This means that Spec(X) is coherent. 
(b) The pullback of analytic subobject of X along f is an analytic subobject of Y. Since affine open subsets form a base for Spec(X), this implies that inverse image of quasi-compact open subset is quasi-compact open. Thus Spec(f) is a mapping of coherent spaces. –

Proposition 5.1.2. (a) If X is quasi-primary then the fraction hull P(X) of X is the intersection of all non-initial analytic monos. 
(b) An object is primary iff its rational hull R(X) is quasi-simple; if X is primary then R(X) = Q(X) = P(X); 
(c) An object is integral iff its rational hull is simple; any integral object X has a generic residue P(X) --> X which is an epic coflat simple fraction. 

Proof. (a) Consider the intersection P of non-initial analytic subobjects of X, which is a non-initial fraction of X containing P(X). We have to prove that P is quasi-simple, or equivalently, that P is pseudo-simple (3.3.10). By (3.3.8.a) it suffices to prove that any non-initial strong subobject of P is unipotent. Since P --> X is coflat, any strong subobject of P is induced from X by (1.5.4). Since any unipotent strong subobject of X induces a unipotent strong subobject of P, we only need to prove that P is disjoint with any non-unipotent strong subobject V of X. Since A is locally disjunctable, V is an intersection of proper disjunctable strong subobjects {V_i}. Since V is non-unipotent, at least one complement (V_i)^c is non-initial, and P  (V_i)^c. Thus P  V = 0. This shows that P is pseudo-simple, thus P = P(X). 
(b) If X is primary then any non-initial analytic mono is epic. Thus R(X) = P(X) by (a), and P(X) is primary by (3.3.8). Any object X is a quotient of its rational hull R(X). If R(X) is quasi-simple, it is primary by (3.3.8), thus X as a quotient of R(X) is primary by (3.2.2.a) 
(c) If X is integral then any proper strong subobject of the reduced object X is non-unipotent by (3.1.2). According to the proof of (a), P(X)  is disjoint with any non-unipotent strong subobject V of X. Since P(X) --> X is coflat, any strong subobject of P(X) is induced from X. This means that the only proper strong subobject of P(X) is 0 , thus P(X) is simple, which is a generic residue of X; and P(X) --> X is an epic coflat fraction as P(X) = R(X)  by (b)and R(X) --> X is epic coflat. Conversely if P(X) is simple the X as a quotient of integral object  R(X) = P(X) is integral by (3.2.3.a). 

Proposition 5.1.3. Suppose X is a quasi-primary object with the fractional hull p_X: P(X) --> X. Let s: S(X) --> X be the strong image of  p_X. 
(a) P(X) is generic quasi-simple and any generic map from a quasi-simple object to X factors through p_X uniquely. 
(b) S(X) is generic primary and any generic map from a primary object to X factors through s uniquely. 
(c) Any quasi-primary object has a unique generic primary strong subobject. 

Proof. (a)  P(X) is generic quasi-simple by  (4.2.5.c). It is easy to see that any generic map from a quasi-simple object to X factors through any non-initial analytic subobject of X, therefore it also factors through the intersection p_X of these analytic monos, which is P(X) by (5.1.2.a). 
(b) The quasi-simple object P(X) is primary (3.3.8), thus its quotient S(X) is also primary. S(X) is a generic strong subobject of X because any non-initial analytic subobject of X contains P(X), therefore not disjoint with S(X). We prove that S(X) has the required universal property. Consider a generic map t: T --> X with T primary. Let p_T: P(T) --> T be the fractional hull of T. Since p_T is generic, so is the composite tp_T. By (a) the generic map t_°p_T: P(X) --> X factors through p_X. Thus tp_T. factors through the strong mono s. Suppose me = t is the epi-strong-mono factorization of t. Since p_T  is epic, mep_T = tp_T is the epi-strong-mono factorization of tp_T. Thus m is the smallest strong mono such that tp_T can be factored through. Since tp_T factors through s, m factors throughout s, thus t =  me factors through s as desired. 
(c) It follows from (b) that S(X) is the unique generic primary strong subobject of X. 

Proposition 5.1.4. (a) Any map f: S --> X with a simple domain factors through a unique residue. 
(b) Any simple subobject is contained in a unique residue. 
(c) A simple subobject is a residue iff it is maximal. 

Proof. (a) The epi S --> f⁺¹(S) is generic by (3.3.4.f), so it factors through the generic residue of f⁺¹(S). The uniqueness follows from (3.4.4.f). 
(b) follows from (a). 
(c) It follows from (b) that any maximal simple subobject is a residue. The other direction has been noticed in (3.4.4.d). 

Proposition 5.1.5. (a) Any colimits of reduced objects is reduced. 
(b) Any cofiltered limits of reduced object is reduced. 

Proof. (a) Since the full subcategory of reduced objects is a coreflective subobject of A , it is closed under colimits. 
(b) Let {r_i: X --> X_i | iI}  be a cofiltered limits of reduced objects in A. We have to prove that any proper strong subobject U of X is non-unipotent. Since any proper strong subobject is contained in a proper regular subobject, and any proper regular subobject is an intersection of proper finitely cogenerated regular subobject by (4.1.3.a), we may assume that U is a finitely cogenerated regular subobject. So let us assume that U is the equalizer of a pair of distinct maps (m, n): X --> T where T is finitely copresentable. Since X is a cofiltered limits and T is finitely copresentable, we can find some t in I and a pair (m_t, n_t): X_t --> T of maps such that m_tr_t = m and n_tr_t = n. We may assume that t is an initial object in I. Let U_t be the equalizer of (m_t, n_t). Then the pullback of U_t along r_t: X --> X_t is U. Since the proper regular subobject U_t is an intersection of proper disjunctable strong subobject, and r_t does not factors through U_t, we can find a proper disjunctable subobject V of X_t containing U_t such that r_t does not factor through r_t. Let V be the pullback of V_t along r_t, and V_i be the pullback of V_t along X_i --> X_t. Then V_i and V are proper disjunctable strong subobjects and U  V, and V^c is the cofiltered limit of (V_i)^c. Since each X_i is reduced and V_i is proper, each (V_i)^c is non-initial. Since the initial object is finitely copresentable, this implies that V^c is non-initial. Thus V is not unipotent, and hence U is not unipotent as desired. 

Proposition 5.1.6. (a) An object is integral iff it is a quotient of a simple object. 
(b) A non-initial object is primary iff it is a quotient of a quasi-simple object. 
(c) An object is reduced iff it is a quotient of coproducts of simple objects. 

Proof. (a) The condition is sufficient because any quotient of a simple object is integral. Conversely any integral object is a quotient of its rational hull, which is simple (5.1.2.c). 
(b) The condition is sufficient because any quotient of a quasi-simple object is primary (3.3.8). Conversely any primary object is a quotient of its rational hull, which is quasi-simple (5.1.2.b). 
(c) Any coproducts of simple objects is reduced (5.1.5.a). Conversely, assume X is a reduced object. Let T be the coproduct of all the residues p_i: P_i --> X of X. Denote by t: T --> X the map induced by p_i. Then T is reduced (5.1.5.a). We prove that t is epic. It suffices to show that t is unipotent as by assumption X is reduced. Any map s: S --> X with a simple domain factors through a unique residue of X by (5.1.4.a). So s factors through t. Since the class of simple objects is unipotent dense, it follows that t is unipotent by (2.2.10).