|
4.3. Extensive Topologies
Suppose A is a coherent analytic category.
Recall that (1.7.4.c) a mono is locally
direct if it is an intersection of direct monos.
Proposition 4.3.1. Any composite of
locally direct mono is a locally direct mono.
Proof. Suppose f: Y --> X is an intersection of
direct monos {fi: Yi --> X |i I},
and we may assume that fi is a cofiltered system. Assume
Y = U + V where U and V are direct subobjects of Y.
Then the unique maps U --> 1 and V --> 1 induce a unique
map t: Y --> 1 + 1. Since 1 + 1 is finitely copresentable,
t factors through Y --> Yr for some r in
I in a map s: Yr --> 1 + 1. The pullbacks
of the injections 1 --> 1 + 1 along s induces a direct sum
Yr = Ur + Vr, and U is the
pullback of Ur along Y --> Yr. Since
Yr is a direct factor of X and Ur
is a direct factor of Yr, Ur is also
a direct factor of X. This shows that any direct factor of Y
is induced from a direct factor of X. Consequently any locally direct
factor of Y is also a locally direct factor of X. I},
and we may assume that fi is a cofiltered system. Assume
Y = U + V where U and V are direct subobjects of Y.
Then the unique maps U --> 1 and V --> 1 induce a unique
map t: Y --> 1 + 1. Since 1 + 1 is finitely copresentable,
t factors through Y --> Yr for some r in
I in a map s: Yr --> 1 + 1. The pullbacks
of the injections 1 --> 1 + 1 along s induces a direct sum
Yr = Ur + Vr, and U is the
pullback of Ur along Y --> Yr. Since
Yr is a direct factor of X and Ur
is a direct factor of Yr, Ur is also
a direct factor of X. This shows that any direct factor of Y
is induced from a direct factor of X. Consequently any locally direct
factor of Y is also a locally direct factor of X.
Definition 4.3.2. (a) A map f:
Y --> X is called indirect
if it does not factors through any proper direct mono.
(b) A non-initial object is called indecomposable
if it has exactly two direct subobjects.
(c) An indecomposable
component of an object X is a locally direct indecomposable
subobject of X.
Proposition 4.3.3. (a) Any map can be
factored uniquely as an indirect map followed by a locally direct mono.
(b) The class of indirect monos is closed under composition.
(c} If P --> X is an indirect map and P is indecomposable,
then X is indecomposable.
(d} Any non-initial object has an indecomposable component.
(e} An indecomposable subobject is a indecomposable component iff it
is a maximal indecomposable subobject.
Proof. (a) Consider a map f: Y --> X. Let u:
U --> X be the intersection of all the direct monos to X such
that f factors through. Then u is a locally direct mono,
and the induced map g: Y --> U is indirect by (4.3.1).
The uniqueness is obvious.
(b) The proof is similar to that of (3.5.4.a).
(c) Suppose U + V = X is a direct sum and U is proper.
Then f-1(U) is a proper direct of P, thus f-1(U)
= 0, i.e. f is disjoint with U, thus f factors
through V. Since f is indirect, we must have V = X,
so U = 0 as desired.
(d) Clearly any simple object is indecomposable. Any non-initial object
has a simple subobject by (4.2.2.d), whose
indirect image in X is indecomposable and locally direct by (c).
(e) is an easy consequence of (b).
Proposition 4.3.4. The extensive topology
on A is spatial
and strict.
Proof. A non-initial object is indecomposable
iff it has exactly two direct subobjects. Thus a non-initial object is
indecomposable iff it determines a one-point-space in the extensive topology.
Clearly any simple object is indecomposable. Thus the direct topology is
spatial by (2.6.5.a) and (4.2.2.d).
By (4.2.2.e) any direct cover of an object X has a finite subcover.
To see that the extensive topology is strict it suffices to consider a
finite direct cover {Ui}: i = 1, ..., n of X.
Suppose Vi is the complement of each Ui.
Let W1 = U1, W2 = V1  U2 , ..., Wi = V1
U2 , ..., Wi = V1  V2 ...
V2 ...  Vi-1 Vi-1  Ui. Then {Wi} is a direct cover of X,
with Wi
Ui. Then {Wi} is a direct cover of X,
with Wi  Wj
= 0 for i < j, and X = Wj
= 0 for i < j, and X = 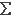 Wi. Let z: Z --> X be the sum of ui:
Ui --> X, and let s: X =
Wi. Let z: Z --> X be the sum of ui:
Ui --> X, and let s: X = 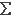 Wi --> Z be the map induced by the inclusion Wi
--> Ui Then z°s
is the identity of X. Thus z is a retraction, hence a regular
epi. This shows that {Ui} is a strict direct cover. Thus
the direct topology is strict.
Wi --> Z be the map induced by the inclusion Wi
--> Ui Then z°s
is the identity of X. Thus z is a retraction, hence a regular
epi. This shows that {Ui} is a strict direct cover. Thus
the direct topology is strict.
If X is any object we denote by B(X) the poset
of direct subobjects of X. The following Proposition 4.3.5 holds
for any extensive category:
Proposition 4.3.5. B(X)
is a Boolean algebra.
Proof. (a) First we show that B(X) is a lattice.
Suppose U and V are two direct subobjects of an object X.
Since finite sums are stable, we have
X = (U + Uc)  (V + Vc) = (U
(V + Vc) = (U  V) + (Uc
V) + (Uc  V) + (U
V) + (U  Vc)
+ (Uc Vc)
+ (Uc  Vc).
Thus
U Vc).
Thus
U  V
and
(U V
and
(U  V) +
(Uc V) +
(Uc  V)
+ (U V)
+ (U  Vc)
are direct objects and
(U Vc)
are direct objects and
(U  V) +
(Uc V) +
(Uc  V)
+ (U V)
+ (U  Vc)
= (Uc Vc)
= (Uc  Vc)c.
Next
(U Vc)c.
Next
(U  V) +
(Uc V) +
(Uc  V)
+ (U V)
+ (U  Vc)
is contained in U Vc)
is contained in U 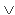 V. Since
(U V. Since
(U  V) + (U V) + (U  Vc) = U and (U
Vc) = U and (U  V) + (Uc
V) + (Uc  V) = V, it also contains U and V. Thus
(U
V) = V, it also contains U and V. Thus
(U  V) +
(Uc V) +
(Uc  V)
+ (U V)
+ (U  Vc)
= U Vc)
= U 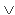 V. V.
Thus B(X) is a lattice with
U  V = U V = U 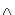 V,
and
(U
V,
and
(U  V) +
(Uc V) +
(Uc  V)
+ (U V)
+ (U  Vc)
= U Vc)
= U 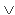 V.
(b) Next we show that B(X) is distributive. If W is
another direct subobject of X, then
X = W V.
(b) Next we show that B(X) is distributive. If W is
another direct subobject of X, then
X = W  Uc + W
Uc + W  U + Wc
implies that
(W
U + Wc
implies that
(W  U)c
= W U)c
= W  Uc
+ Wc.
Thus
(W Uc
+ Wc.
Thus
(W  U)c U)c  W = [(W
W = [(W  Uc)
+ Wc] Uc)
+ Wc]  W
= W W
= W  Uc Uc W + Wc
W + Wc  W
= W W
= W  Uc.
Similarly
(W Uc.
Similarly
(W  V)c V)c  W = W
W = W  Vc.
We have Vc.
We have
W  (U
(U 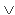 V) V)
= W  [(U [(U  V) + (Uc
V) + (Uc  V) + (U
V) + (U  Vc)] Vc)]
= W  U U  V + W
V + W  Uc Uc  V + W
V + W  U U  Vc
Vc
= W  U U  V + (W
V + (W  Uc) Uc)  V + W
V + W  (U (U  Vc).
Vc).
= (W  U) U)  (W
(W  V) + ((W V) + ((W  U)c
U)c  W) W)  V + U
V + U  (W (W  (W
(W  V)c) V)c)
= (W  U) U)  (W
(W  V) + (W V) + (W  U)c
U)c  (W (W  V) + (W
V) + (W  U) U)  (W
(W  V)c V)c
= (W  U) U) 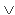 (W
(W  V). V).
This shows that B(X) is a distributive lattice. Clearly
Uc is the complement  U
of U in the lattice B(X). Thus B(X)
is a Boolean algebra. U
of U in the lattice B(X). Thus B(X)
is a Boolean algebra.
Remark 4.3.6. Consider the canonical
functor J: FiniteSet --> A
which preservs finite limits and sums. For each object X in A
the pullback of the finite-limit-preserving functor homA
(X, ~) along J is a finite-limit-preserving functor FiniteSet
--> Set, thus determines a Boolean algebra, which is precsely B(X).
This argument holds for any extensive category with a terminal object 1.
Recall that (2.6.6) the extensive topology  E
on A is the framed topology E
on A is the framed topology  E
generated by the divisor E of direct
monos. E
generated by the divisor E of direct
monos.
Proposition 4.3.7. (a) A finite set
{Ui} of direct subobjects of an object X is a
unipotent cover iff the join of {Ui} is X.
(b)  E(X)
is isomorphic to the frame of ideals of the Boolean algebra B(X). E(X)
is isomorphic to the frame of ideals of the Boolean algebra B(X).
(c) There is a bijection between the set of indecomposable components
and the set of prime ideals (or ultrafilters) of B(X).
Proof. (a) Suppose {Ui} is a finite unipotent
cover of X. Let V be the join of {Ui}.
Then Vc is disjoint with each Ui, so
Vc = 0 and V = X. Conversely, suppose the join
of a finite set {Ui} of direct subobjects is X.
Suppose t: T --> X is disjoint with each Ui.
Then t factors through each (Ui)c.
Thus t factors through  (Ui)c = (
(Ui)c = (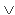 Ui)c = Xc = 0. Thus t
is initial, i.e. {Ui} is a unipotent cover over X.
Ui)c = Xc = 0. Thus t
is initial, i.e. {Ui} is a unipotent cover over X.
(b) It follows easily from (a) that if U
is an E-sieve then the collection of direct monos in U
is an ideal of B(X), and the resulting map  E(X)
--> B(X) is an isomorphism. E(X)
--> B(X) is an isomorphism.
(c) If P is an indecomposable component of X then the
set V of direct subobjects containing P is a prime filter
(ultrafilter) of B(X). For if U is a direct subobject
not containing P, then Uc contains P as
it is indecomposable. Conversely, if V is a ultrafilter of B(X)
then the intersection P of direct subobjects in V is non-initial
as 0 is finitely copresentable, and P is locally direct.
If U is a proper direct subobject of P then U is also
a locally direct subobject of X, thus there is a proper direct subobject
W of X such that W  P is a proper direct subobject contains U. Since V is
an ultrafilter, W is not in V implies that Wc
is in V. It follows that P is contained in Wc.
Thus P
P is a proper direct subobject contains U. Since V is
an ultrafilter, W is not in V implies that Wc
is in V. It follows that P is contained in Wc.
Thus P  W = 0, which
implies that U = 0. This shows that P is an indecomposable
component of X. Suppose V and V' are two different
ultrafilters of B(X) and P and P' are the corresponding
indecomposable components. If T is a direct subobject in V
not in V' then Tc is in V'. Thus P
is contained in T and P' is contained in Tc,
which implies that P and P' are disjoint. This shows that W = 0, which
implies that U = 0. This shows that P is an indecomposable
component of X. Suppose V and V' are two different
ultrafilters of B(X) and P and P' are the corresponding
indecomposable components. If T is a direct subobject in V
not in V' then Tc is in V'. Thus P
is contained in T and P' is contained in Tc,
which implies that P and P' are disjoint. This shows that  E(X)
is isomorphism to B(X). E(X)
is isomorphism to B(X).
Corollary 4.3.8.
(a) The space pt( E(X))
of E(X))
of  E(X)
is homeomorphic to the space of prime ideals of the Boolean algebra B(X),
thus is a Stone space (see [Johnstone
1982, p.62-75]). E(X)
is homeomorphic to the space of prime ideals of the Boolean algebra B(X),
thus is a Stone space (see [Johnstone
1982, p.62-75]).
(b) The extensive topology on a coherent analytic category is a strict
metric site, which may be interpreted as the functor sending each object
X to the Stone space of the indecomposable components of X.
[Next Section][Content][References][Notations][Home]
|