2.2. Normal Monos 

Definition 2.2.1. (a) A set S of maps to an object X is called a unipotent cover on X if 0 --> X is the only map that is disjoint with S. 
(b) A map to X is unipotent if it is a unipotent cover on X. 

The term " unipotent " is suggested by the following (2.2.2) and (2.2.2.1): 

Remark 2.2.2. Suppose S is a set of maps to X. Then by (2.1.1) we have 
(a) S is unipotent iff S = 0X. 
(b) S is unipotent iff S = 1X. 

Example 2.2.2.1. Consider a homomorphism of commutative rings : A --> B. The induced morphism Spec(): Spec (B) --> Spec (A) is unipotent in the category of affine schemes iff the kernel of  is a nilpotent ideal. This suggests that the dual of unipotent map is called a nilpotent map. 

Unipotent covers (resp. unipotent maps) play the important role of surjective covers (resp. maps) in categorical geometry. For instance, a map in the categories of sets, topological spaces and affine schemes is unipotent iff it is surjective, and this is true for most of natural metric sites. 

Proposition 2.2.3. (a) Isomorphisms are unipotent maps. 
(b) Any pullback of a unipotent map is unipotent. 
(c) Composites of unipotent maps are unipotent. 
(d) If f: Y --> X and g: Z --> Y are two maps and f°g is unipotent then f is unipotent. 
(e) 0 --> X is unipotent iff X = 0. 

Proof. (a) is obvious. 
(b) Suppose v: V --> Y is the pullback of a unipotent map u: U --> X along a map f: Y --> X. Consider a non-initial map t: T --> Y. Since u is unipotent, the non-initial map ft is not disjoint with u, thus we can find a non-initial map s: S --> T such that fts factors through u. Since v is a pullback of u along f, we can find a map r: S --> V such that ts = vr. This shows that t is not disjoint with v. Hence v is unipotent. 

(c) Suppose f: Y --> X and g: Z --> Y are two unipotent maps. Consider a non-initial map t: T --> X. Since f is a unipotent cover on X, t is not disjoint with f. Thus we can find a non-initial map u: S --> T such that tu factors through f in a map s: S --> Y. Since g is unipotent and s is non-initial, we can find a non-initial map v: R --> S such that sv factors through g in a map r: R --> Z. The non-initial map tuv = fgr factors through t and fg. This shows that any non-initial map t to X is not disjoint with fg, i.e. fg is unipotent. 
(d) Assume fg is unipotent. If t: T --> X is a non-initial map. We can find a non-initial map u: R --> T such that tu factors through fg. Then tu also factors through f. This shows that f is unipotent. 
(e) If 0 --> X is unipotent then X = 0 because the identity map 1X: X --> X is disjoint with 0 --> X. 

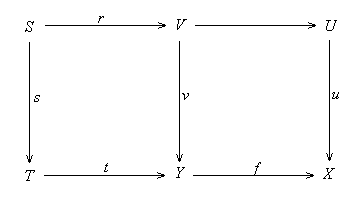
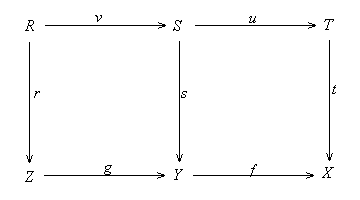
Proposition 2.2.4. Suppose f: Y --> X is a map. Suppose S and T are two sets of maps to Y. Write f*(S) for the set {fu | u  S}. 
(a) If T  S then f*(T)  f*(S). 
(b) If f is a mono and f*(T)  f*(S) then T  S. 

Proof. (a) Assume T  S. Consider a map t: T --> Y in T. Since t  S, for any non-initial map s: S --> T we can find a non-initial map w: W --> S such that tsw factors through some map v: V --> Y in S. Then the non-initial map ftsw factors through the map fv in f*(S). Thus f°t  f*(S). Since this is true for any t in T, we obtain f*(T)  f*(S). 

(b) If f is a mono then we can reverse the above proof for (a). 

Definition 2.2.5. A mono u: U --> X is normal if u generates the normal sieve {u} (i.e. sieve(u) = {u}). Equivalently, u is normal iff t  {u} implies that t factors through u. 

Proposition 2.2.6.  (a) Isomorphisms and initial maps are normal monos. 
(b) Any normal unipotent mono is an isomorphism. 
(c) Composites of normal monos are normal monos. 
(d) The pullbacks of normal monos are normal monos. 
(e) Any intersection of normal monos is a normal mono. 
(f} Any complement of a mono is a normal mono. 

Proof. (a) is obvious. 
(b) If u is a normal unipotent mono then u generates the unit sieve 1X by (2.2.2.b) and (2.2.5), thus is an isomorphism. 
(c) Suppose f: Y --> X and g: Z --> Y are two normal monos. Suppose a map t: T --> X is in {fg}. Then t  {t}  {fg} {f}by (2.1.1.c). Since f is normal, t factors through f in a map s: T --> Y. Since f is a mono, by (2.2.4.b) t = fs   fg implies that s  s  g. Since g is normal, s factors through g in a map r: T --> Z. Thus t = fgr factors through fg. This shows that fg is normal. 

(d) follows (2.1.3.b). 
(e) follows from (2.1.2.b). 
(f) follows from (2.1.2.a). 

Corollary 2.2.7. If A is an analytic category then any singular or analytic mono is normal. 

Proposition 2.2.8. If A has pullbacks, then a mono is normal iff its pullback along any map is not proper unipotent. 

Proof. Suppose u: U --> X is a mono. If u is normal then any pullback of u is normal by (2.2.6.d), thus not proper unipotent by (2.2.6.b). Conversely, assume the condition is satisfied. If t: T --> X is a map in {u}, then its pullback along u is normal unipotent, thus an isomorphism by (2.2.6.b), which implies that t factors through u. This shows that u is normal. 

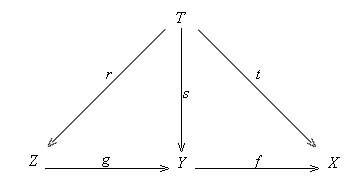
Definition 2.2.9. A class of objects is called uni-dense if any non-initial object is the codomain of a map start from a non-initial object in the class. 

Proposition 2.2.10. Suppose C is a uni-dense class of objects. A map f: Y --> X is unipotent iff any map from a non-initial object in C to X is not disjoint with f. 

Proof. The condiiton is clearly necessary. Conversely, assume the condition is satisfied. If t: T --> X is a non-initial map, then there is a non-initial map r: R --> T with the domain T in C. Now tr is not disjoint with f, so t is not disjoint with f. 

 
 
 
 [Next Section][Content][References][Notations][Home]