Definition 4.2.1. A category is coherent if it salsifies the following conditions: 
(a) It is locally finitely copresentable. 
(b) Finite sums are stable disjoint. 
(c) The sum of the terminal object with itself is finitely copresentable. 

A category is a coherent analytic category iff its opposite is a locally indecomposable category  in the sense of Diers [1986]. A locally finitely copresentable category is a coherent analytic category iff its full subcategory of finitely copresentable objects is lextensive. This was proved by Diers in [Diers 1983] in the dual situation. 

Example 4.2.1.1. (see [Johnstone, 1982]) Recall that an open subset is quasi-compactif every open cover has a finite subcover (note that in [Johnstone 1982] quasi-compact open subset is simply called compact). If X is a topological space we denote by ^c(X) the family of quasi-compact open subsets of X, then ^c(X) is closed under finite unions. A sober topological space X is coherentif ^c(X) is closed under finite intersection (this is equivalent to that ^c(X) is a distributive lattice), and forms a base for the  topology on the space. A continuous mapping f: X --> Y of two coherent spaces is called coherent if f^-1(U) is quasi-compact for any quasi-compact open subset U of Y. A coherent space X is uniquely determined by the distributive lattice ^c(X). In fact, according to Stone's representation theorem for distributive lattices, the category of coherent spaces CohSp is dual to the category of distributive lattices DLat. Since DLat is locally finitely presentable (in fact, finitary algebraic), CohSp is locally finitely copresentable. Clearly finite sums in CohSp are stable disjoint and the space of two points is finitely copresentable, thus CohSp = DLat^op is a coherent analytic category. 

Suppose A is a coherent analytic category. 

Proposition 4.2.2. (a) A is a spatial analytic category. 
(b) The initial object 0 is finitely copresentable. 
(c) The initial subobject 0 --> X of any subobject X is finitely cogenerated. 
(d) Any non-initial object has a simple (resp. an extremal simple) strong subobject. 
(e) Any analytic cover of an object has a finite analytic subcover. 
(f) Any monic divisor on A is spatial. 

Proof. (a) A coherent analytic category is a perfect analytic category by (4.1.2). It is spatial by the assertion (d) and (2.6.5.a). 
(b) The initial object 0 is the kernel of the injections 1 --> 1 + 1. Since 1 and 1 + 1 are finitely copresentable, and the full subcategory of finitely copresentable objects is closed under finite limits by (4.1.2.c), it follows that 0 is also finitely copresentable. 
(c) Suppose 0 is the intersection of a collection u_i: U_i --> X of strong subobjects. Let v_j: V_j --> X be the collection of finite intersections of u_i. Then 0 is the cofiltered limit of {v_j}. Since 0 is finitely copresentable, the identity 0 --> 0 factors through some 0 --> v_j in some map v_j --> 0. Since 0 is a strict initial, this implies that v_j = 0. This shows that 0 is a finitely cogenerated subobject by (4.1.4). 
(d) Consider a non-initial object X. Let S* be the set of non-initial strong subobject of X. It is non-empty. A strong subobject of X is simple iff it is a minimal element of S*. Let C be a chain in S*. Let us assume that the intersection of subobjects in C is 0. Since 0 is finitely cogenerated by (c), there is a finite subset C₀ of C whose intersection is 0 by (4.1.4). But the intersection of C₀ is an element of C. We obtain a contradiction. By Zorn's lemma, S* has a minimal element, which is a simple object. The proof for the case of extremal simple objects is similar. 
(e) Suppose {V_i} is a set of disjunctable strong subobjects such that {(V_i)^c| i I} is an analytic cover for X. Let V be the intersection of these {V_i}. Then by (3.1.10) we have X = 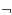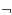{(V_i)^c} = 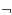V, so V = 0. By (c) there is a finite subset J  I such that {V_i| i J} has intersection 0. Applying (3.1.10) again we see that {(V_i)^c} is a finite analytic cover for X. 
(f) follows from (d) and (2.6.5.a) because the locale of any extremal simple object for any monic divisor is 2 (i.e. the locale of one-point-space). 

Proposition 4.2.3. (a) Cofiltered limits and products of coflat maps are coflat. 
(b) Intersections of coflat monos are coflat monos. 
(c) Intersections of fractions are fractions. 
(d) Intersections of epic fractions are epic fractions. 

Proof. (a) Consider a cofiltered diagram of coflat maps (f_i: X_i --> Y_i | i  I}, whose limit is f: X --> Y with the projections (s_i: X --> X_i, t_i: Y --> Y_i}. For any i  I let f_i': X_i' --> Y be the pullback of f_i along t_i. Then f is a cofiltered limit of {f_i'}. Let m: (U, u) --> (V, v) be an epi in A/Y. Denote the pullback of m along f_i' by m_i':(U_i, x_i) --> (V_i, v_i) and the pullback of m along f by m':(U', u') --> (Y', y'). As pullbacks commute with limits, m is the limit of {m'}. As f_i' is coflat and m is epic, each m_i' is epic. Since any cofiltered limit of epis is epic in a locally finitely copresentable category, m' is epic (cf. [Adamek and Rosicky 1994]). As a result, f is coflat. The second assertion follows from the fact that a product of coflat maps is a cofiltered limit of finite products of coflat maps, therefore is coflat. 
(b) follows from (a). 
(c) Since any intersection of normal monos is normal, the assertion follows from (b). 
(d) First in an analytic category any finite intersection of epic coflat monos is epic (as it is the pullback of an epi along coflat maps). Since an arbitrary intersection is a cofiltered intersection of finite intersections, and any cofiltered limit of epis is epic (in a locally finitely copresentable category), it follows from (c) that the intersection of epic fractions is epic. 

Definition 4.2.4. (a) An object is rationally closed if any epic fraction to it is an isomorphism. 
(b) An object is analytically closed if any epic analytic mono to it is an isomorphism. 

Proposition 4.2.5. (a) Any object X has a unique rationally closed epic fraction R(X). 
(b) Any object X has a unique analytically closed epic preanalytic fraction Q(X). 
(c} Any quasi-primary objectX has a unique generic quasi-simple fraction P(X). 

Proof. (a) The intersection of epic fractions of an object X is an epic fraction R(X) by (4.2.3.d). Since any composition of epic fractions is an epic fraction, clearly R(X) is rationally closed. Any rationally closed epic fraction of X must be the intersection of all the epic fractions of X, thus is unique. 
(b) The intersection of epic preanalytic fractions of an object X is an epic preanalytic fraction Q(X) by (4.2.5.e). Since any composition of epic preanalytic fractions is an epic preanalytic fraction, clearly Q(X) is analytically closed. Any analytically closed epic fraction of X must be the intersection of all the epic preanalytic fractions of X, thus is unique. 
(c) The intersection of any two non-initial fractions of a quasi-primary object X is non-initial by (3.5.8). Thus the intersection of all the non-initial fractions of X is a non-initial fraction P(X) because 0 is finitely copresentable. Clearly P(X) is generic. Since any composition of fractions is a fraction, clearly P(X) is quasi-simple. Any quasi-simple fraction of X must be the intersection of all the fractions of X, thus is unique. 

Definition 4.2.6. (a) The unique rationally closed epic fraction R(X) of an object X is called the rational hull of X. 
(b) The unique analytically closed epic preanalytic fraction Q(X) of an object X is called the called the analytic hull of X. 
(c) The unique quasi-simple fraction P(X) of a quasi-primary object X is called the fractional hull of X. 

Recall that a map to an object X is called prelocal if it does not factor through any proper analytic mono to X. 

Definition 4.2.7. A preanalytic mono is a map such that any of its pullbacks is not proper prelocal. 

Proposition 4.2.8. (a) Any preanalytic mono is a mono; any analytic mono is preanalytic. 
(b) An prelocal preanalytic mono is an isomorphism. 
(c) Any pullback of a preanalytic mono is a preanalytic mono. 
(d) Any composite of preanalytic monos is a preanalytic mono. 
(e) Any intersection of preanalytic monos is a preanalytic mono. 
(d) Any non-isomorphic preanalytic mono factors through a non-isomorphic analytic mono. 
(e) A map is not prelocal iff it factors through a non-isomorphic preanalytic mono. 

Proof. Similar to (1.1.2) and (1.1.3). 

Proposition 4.2.9. (a) The class of preanalytic mono is the smallest class of monos containing the class of analytic monos which is closed under composition and arbitrary intersection. 
(b} Any preanalytic mono is a fraction. 

Proof. (a) Consider a class S of monos which is closed under composition and intersection. Assume S contains the class of analytic monos. We prove that S contains the class of preanalytic monos. Consider a preanalytic mono u: U --> X. Let v: V --> X be the intersection of all the monos to X in S through which u factors. Then v is a mono in S through which u factors in the form u = ve therough a mono e: U --> V. If w is an analytic mono to V through which e factors, then vw is a mono in S through which u factors. Since by assumption v is the intersection of such monos, vw factors through v. Thus w is an isomorphism, which means that e is a prelocal map. But u: U --> X is preanalytic implies that e: U --> V is preanalytic by (4.2.8.c), thus e is an isomorphism by (4.2.8.b). Since v  is in S, the relation u = ve implies that u is in S. 
(b) The class of coflat (resp. normal) monos is closed under composition and intersection and any analytic mono is coflat. By (a) these two classes of maps contain the class of preanalytic monos. Thus any preanalytic mono is coflat and normal. 

Remark 4.2.9. Suppose f: Y --> X is a map. If f = gl with l: Y --> Z a quasi-local (resp. prelocal) map and g: Z --> X a fraction (resp. analytic mono), then we say that (l, g) is a quasi-local-fraction (resp. prelocal-preanalytic) factorization of f, and Z is the quasi-local (resp. prelocal) image of Y in X. It is easy to see that g is the intersection of all the fractions (resp. presingular monos) to X such that f factors, thus such a factorization is unique. As in the case of epi-strong-mono factorization, quasi-local-fraction factorizations and prelocal-presingular factorizations exist because these classes of monos are closed under composition and intersection.