2. Ideals 

Let C be a category. 

If (r1 , r2): Y --> X is a pair of parallel arrows then we say that r = (r1, r2) is a 2-arrow in C; the common domain (resp. codomain) of r1 and r2 is called the domain (resp. codomain) of r. A 2-arrow r = (r1, r2) is uniform if r1 = r2. Any ordinary arrow t: Y --> X (also called a 1-arrow) determines a uniform arrow (t, t): Y  --> X . 

It is obvious how to define the compositions of 2-arrows: 

If r = (r1, r2): Y --> X and s = (s1, s2): Z  --> Y are two 2-arrows we define rs to be the 2-arrow 

rs = (r1s1, r2s2): Z  --> X.
With these 2-arrows we obtain a new category C2 having the same objects as C. The original category is naturally a subcategory of this new category if we identify each 1-arrow t with the uniform arrow (t, t). 

A 2-arrow with X as codomain is called a 2-element of X. Denote by 1X the set of 2-elements of X. 

Any arrow f: Y  --> X determines a map 1Y  --> 1X sending each 2-element r of Y to the 2-element fr of X. We simply write f for this map. 

Denote by 0X (or simply 0) the set of uniform 2-elements of X. Note that 0X is non-empty because it contains the uniform 2-element (1X, 1X). If f: Y --> X is an arrow then the subset f-1(0) is called the 2-kernel of f, denoted by ker(f). 

Definition 2.1. (a) A set of 2-elements of X is called a 2-kernel if it is the 2-kernel of some arrow t: X  --> Z. 
(b) A set a of 2-elements of X is called a 2-ideal (or simply ideal ) of X if it is an intersection of some 2-kernels. 

Denote by I(X) the set of ideals of X. 

Remark 2.2. (a) A set a of 2-elements of X is an ideal if and only if there is a collection {hi: X  --> Zi} of arrows such that 

a =  iker(hi) = {r  1X | hir1 = hir2 for all i}. 

(b) An ideal of X is a sieve on X as an object in C2. 

The collection of ideals is closed under intersection in 1X. Thus I(X) is a complete lattice with 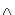 = . Any set T of 2-elements of X generates an ideal (T) of X, which is the intersection of all the ideals (or 2-kernels) containing T. An ideal of an object X is called a 2-principal ideal if it is generated by a 2-element of X. 

Remark 2.3. (a) Any ideal is an intersection of 2-kernels. 
(b) Any ideal is a join of 2-principals. 
(c) Suppose any pair of parallel arrows has a coequalizer. Then any 2-principal is a 2-kernel. Thus any ideal is a join of 2-kernels. 
(d) Suppose any arrow has a kernel pair. Then any 2-kernel is a 2-principal ideal. Thus any ideal is an intersection of 2-principles. 
(e) If finite limits and finite colimits exist, then the set of 2-kernels and that of 2-principals are identical. 

Example 2.3.1. (a) 0 is the smallest ideal of X. 
(b) The set 1X is the largest ideal of X (take an empty {hi}), called the unit ideal of X. 
(c) An ideal a of X is called proper if a 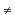 1X . 

Remark 2.4. Suppose f: Y  --> X is an arrow. 
(a) If g: X --> Z is any arrow, then 

(gf)-1(0X) = f-1(g-1(0X)) = f-1(ker(g)).
It follows that if a is a 2-kernel of X, then f-1(a) is a 2-kernel of Y. Since any ideal a of X is an intersection of 2-kernels ai, we have 
f-1(a) = f-1(Ç ai) = Ç (f-1(ai).
Thus f-1(a) is an ideal. We obtain a mapping I(X) --> I(Y) sending each ideal a of X to the ideal f-1(a) of Y, denoted also by f-1. Clearly f-1: I(X)  --> I(Y) preserves intersections (i.e. meets) of ideals. 
(b) If S is any set of 2-elements of X, the image f(S) generates an ideal of Y, denoted by (f(S)). We obtain a mapping f*: I(Y) --> I(X) sending each ideal a of Y to the ideal f*(a) = (f(a)). 
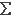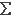(c) Since f* is the left adjoint of f-1, it preserves joins. Thus if {ai} is a set of ideals of X and  ai is the ideal generated by  ai, then f*( ai) = 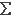 f*(ai). 

Remark 2.5. Suppose f: Y --> X is an arrow and S is a set of 2-elements of Y. Denote by (S) and (f(S)) the ideals generated by S and f(S) respectively. Then f*((S)) = (f((S))) = (f(S)). 

Remark 2.6. Suppose f: X --> Y is an arrow. Then 
(a) f*(0) = 0. 
(b) f-1(1) = (1). 
(c) f*(1) = 0 if and only if f-1(0) = 1, i.e. ker(f) = 1. 
(d) If a is a proper ideal of X then there is an arrow f: X  --> Z such that f*(a) = 0 and f*(1) 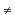 0 (thus 0  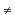1  I(Z)). 

Remark 2.7. The following are equivalent for an arrow f: Y  --> X: 
(a) f is a monomorphism. 
(b) ker(f) = 0. 
(c) f: 1Y -->  1X is injective. 
(d) f is a monomorphism in the category C2. 

Next we shows that the notion of unitary arrow introduced in (1.3) can also be defined in terms of ideals (note that here by null or unitary we always mean right null and right unitary): 

Proposition 2.8. (a) An arrow t: X  --> T is null if and only if t*(1) = 0 (i.e. ker(t) = 1). 
(b) An object Z is null if and only if Z has only one ideal (i.e. 0 = 1 is the only ideal). 
(c) An arrow f: Y  --> X is unitary if and only if f*(1) = 1. 
(d) An object X is unitary if and only if the codomain of any arrow t: X  --> T with t*(1) = 0 is terminal. 

Proof. (a) t is null if and only if t(1X)  0, i.e. t*(1) = 0, or equivalently, ker(t) = 1. 
(b) Z is null if and only if any 2-element of Z is uniform, i.e. 0 = 1. 
(c) We have f*(1) = 1 if and if there is no arrow t: X --> Z such that t*(f*(1) = 0 and t*(1) 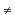 0 by (2.6.d). By (a) this is equivalent to that there is no arrow t: X  --> Z such that tf is null but t is not null, i.e. f is unitary. 
(d) follow from (a) and the definition of a unitary object. n 

Remark 2.9. (a) If f: Y  --> X is not unitary then there is an arrow g: X  --> Z such that Z is not null and (gf)*(1) = 0 (this follows from (2.6.d) and (2.8.c)). 
(b) It follows from (a) that a category is unitary if and only if f*(1) 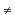 0 for any arrow f: X  --> Z with Z non-terminal. 

Proposition 2.10. An object is simple if and only if it is unitary with exactly two ideals. 

Proof. (a) Note that the condition (1.11.a) in the definition of a simple object is equivalent to that 0 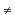 1 for X. If X is simple then these two ideals are the only 2-kernels of X. Since any ideal is an intersection of 2-kernels, these are the only ideals of X. Also X is unitary by (1.13). 
Conversely assume X is unitary with exactly two ideals. Then (1.11.a) holds as mentioned above. If f: X  --> T is an arrow to a non-terminal object T, then f is not null, thus ker(f) = 0, which means that f is monomorphic. n 

Corollary 2.11. An object in a unitary category is simple if and only if it has exactly two ideals. n 
  

[Next Section][Content][References][Notations][Home]