Let C be any category. 

A set of 2-elements of an object X is called invertible if it generates 1_X . A proper ideal of X is called maximal  if it is not contained in any other proper ideal of X. Recall that an object with exactly two ideals is called a simple object. 

Remark 3.1. (a) Suppose X is an object such that the product X  X exits. Then the 2-element (p₁, p₂): X  X --> X of projections is invertible. 
(b) Suppose S is a set of 2-elements of Y and f: Y --> X is an arrow. Then t(S) is invertible if and only if f((S)) or f*((S)) = (f((S))) is invertible. 

Proposition 3.2. (a) Any maximal ideal is a 2-kernel. 
(b) Suppose m is a maximal ideal of X and S is a set of 2-elements of X not contained in m. Suppose t: X --> Z is an arrow such that m = ker(t). Then t(S) is invertible. 

Proof: (a) Any ideal is an intersection of 2-kernels. Thus any maximal ideal must be a 2-kernel. 
(b) Since m and S generate 1_X, t(m) and t(S) generate 1_Z. Since (t(m))  0_Z, we must have (t(S)) = 1_Z. Thus t(S) is invertible. 

Definition 3.3. (a) An ideal a of an object X is called radical if for any 2-element r Ï a there exists an arrow t: X --> Z such that t(r) is invertible and t(a) is non-invertible. 
(b) An object X is called reduced if 0_X is radical. 
(c) A unitary category is called reduced if each object is reduced. 

Proposition 3.4. (a) Any maximal ideal is radical. 
(b) Any simple object is reduced. 

Proof. (a) This follows from (3.2). 
(b) Since 0 is a maximal ideal of a simple object, it is radical. Thus any simple object is reduced. 

Proposition 3.5. (a) Intersections of radical ideals are radical. 
(b) If f: Y --> X is an arrow and a is a radical ideal of X then f^{- 1}(a) is a radical ideal of Y. 
(c) If f: Y --> X is an arrow with X reduced then ker(f) is radical. 
(d) If f: Y --> X is a monomorphism and X is reduced then Y is reduced (i.e., any subobject of reduced object is reduced). 

Proof. (a) First note that 1_X is always radical. Suppose a is the intersection of a set {a_i} of radical ideals of X. We may assume a is proper. If a 2-arrow r is not in a, then r is not in a_i for some i. Since a_i is radical we can find an arrow t: X --> Z such that t(r) is invertible and t(a_i) is not. Since a  a_i, t(a) is non-invertible. This shows that a is radical. 
(b) Suppose r is a 2-element of Y not in f^-1(a). Then f(r) is not in a. Since a is radical, we can find an arrow t: X --> Z such that t(f(r)) is invertible and t(a) is non-invertible. Then (tf(r)) is invertible and (tf)(f^-1(a)) is not. This shows that f^-1(a) is radical. 
(c) If X is reduced then 0_X is radical. Thus ker(f) = f^-1(0_X) is radical by (b). 
(d) If f: Y --> X is a monomorphism then 0_Y = ker(f) = f^-1(0_X). Thus 0_Y is radical if 0_X is radical by (c). 

For any set S of 2-elements of an object X we denote by (S) the set of 2- elements r of X such that, if t: X --> Z is an arrow and t(r) is invertible, then t(S) is invertible. Let r(S) be the intersection of all the radical ideals containing S. It follows from (3.1.b) that (S) = ((S)) and r(S) = r((S)). 

Remark 3.6. If {a_i} is a set of ideals X then r(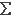 a_i) = r( 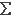r(a_i)). Denote by I^r(X) the set of radical ideals of X. This means that r: I(X) ® I^r(X) preserves joins. 

Remark 3.7. Suppose a and b are two ideals of X. 
(a) We have a  (a) Í r(a). 
(b) a is radical if and only if a = (a) = r(a). 
(c) If a  b then (a)  Ö(b) and r(a)  r(b). 
(d) If a b and b is radical then (a)  r(a)  b. 
(e) If b is not contained in (a), then there is an arrow t: X --> Z such that t(b) is invertible and t(a) is not. 

Definition 3.8. A unitary category is called radical if any non-terminal object has a proper radical ideal. 

Suppose C is a radical category. 

Proposition 3.9. Suppose a is a proper ideal of an object X and t: X --> Z is an arrow. Then 
(a) a is contained in a proper radical ideal of X. 
(b) If t(a) is not invertible, then there is a proper radical ideal b containing a and t(b) is not invertible. 
(c) (a)= r(a). 
(d) t(r(a)) is invertible if and only if t(a) is invertible. 
(e) r(f(r(a))) = r(f(a)). 

Proof. (a) Since a is proper it is contained in a proper kernel ker(t) for an arrow t: X --> Z such that Z is non-null. Since C is radical Z has a proper radical ideal b. Then t^-1(b) is a proper radical ideal containing a. 
(b) By (a) we can find a proper radical ideal c of Z containing (t(a)). Then b = t^-1(c) is a proper radical ideal of X containing a and t(b) Í c is non-invertible. 
(c) We only need to prove that (a)  r(a). Suppose r  (a). Then there is an arrow t: X --> Z such that t(r) is invertible and t(a) is not. Then by (b) we can find a radical ideal b containing a and t(b) is non-invertible. Since t(r) is invertible we must have r Ï b. Thus r  r(a). This shows that (a)  r(a). 
(d) We only need to show that if t(r(a)) is invertible then t(a) is invertible. If t(a) is non-invertible then by (b) we can find a radical ideal b containing a such that t(b) is non-invertible. Since b  r(a), t(r(a)) is non-invertible. 
(e) follows from (d). 

Corollary 3.10. If a  is an ideal of an object X then r(a) = 1 if and only if a = 1. 

Proof. This follows from (3.9.a) that any proper ideal is contained in a proper radical ideal. 

Proposition 3.11. Suppose a and b are two proper ideals of an object X. Then the following conditions are equivalent: 
(a) r(a) = r(b). 
(b) For any arrow f: X --> Z,  f(r(a)) is invertible if and only if f(r(b)) is invertible. 
(c) For any arrow f: X --> Z, f(a) is invertible if and only if f(b) is invertible. 

Proof. (a) and (b) are equivalent by (3.9.c) and (3.7.e). The assertions (b) and (c) are equivalent by (3.9.d). 

Proposition 3.12. A unitary category C is reduced if and only if any ideal of an object is radical. 

Proof. If the condition holds then the ideal 0_X for any object X is radical, which implies that C is reduced. Conversely assume C is a reduced category. Then any 2- kernel of an object is radical by (3.5.b). Since any ideal is an intersection of 2-kernels, it is radical by (3.5.a).