1. Metric Sites
Definition 1.1. Let C
be a category. A metric pretopology  on C consists of the data
on C consists of the data
(a) for every object X  C, a topological space
C, a topological space  (X),
and (X),
and
(b) for every morphism f: Y --> X in C,
a continuous function  (f): (f):  (Y)
--> (Y)
-->  (X), (X),
subject to the conditions
(1)  (1X)
is the identity of (1X)
is the identity of  (X). (X).
(2)  (gf)
= (gf)
=  (g) (g) (f)
whenever gf is defined. (f)
whenever gf is defined.
Alternatively one can define a metric pretopology  on C to be a functor from C to the metacategory
of topological spaces (cf. [Mac Lane
1971, p.9]). The set
on C to be a functor from C to the metacategory
of topological spaces (cf. [Mac Lane
1971, p.9]). The set  (C)
of topological spaces together with all the continuous
functions (C)
of topological spaces together with all the continuous
functions  (f) is a category,
thus t may be viewed as a functor
from C to the category (f) is a category,
thus t may be viewed as a functor
from C to the category  (C). (C).
Definition 1.2. A metric
presite is a pair (C,  )
consisting of a category C and a metric pretopology )
consisting of a category C and a metric pretopology  on C; C is called the underlying category of (C,
on C; C is called the underlying category of (C,  ). ).
Suppose (C,  )
is a metric presite. We often simply write C for (C, )
is a metric presite. We often simply write C for (C,  ).
If X is an object and f: Y
--> X a morphism, we shall adopt the following notation: ).
If X is an object and f: Y
--> X a morphism, we shall adopt the following notation:
|X| (or simply X) for the underlying space  (X)
(a subset U of |X| is often called a subset
of X); (X)
(a subset U of |X| is often called a subset
of X);
|f| (or simply f) for the underlying map
t(f);
|f(X)| for the subset |f|(|X|)
of |Y|;
f(U) for |f|(U) if U  |Y|, and f-1(V) for |f|-1(V)
if V
|Y|, and f-1(V) for |f|-1(V)
if V  |X|. |X|.
We say f: Y --> X is surjective,
injective, homeomorphism,
bicontinuous, open,
closed, etc., if the
underlying map |f|: |Y| --> |X| is so. An object
X is called an empty object
if the underlying space |X| of X is empty.
A morphism f: Y --> X is called active
if any morphism g: Z --> X with |g(Z)|  |f(Y)| factors through f uniquely.
An effective
morphism is an active morphism f: Y --> X
such that the continuous map |f|: |Y|
-->|X| is an embedding (i.e., f is bicontinuous).
|f(Y)| factors through f uniquely.
An effective
morphism is an active morphism f: Y --> X
such that the continuous map |f|: |Y|
-->|X| is an embedding (i.e., f is bicontinuous).
A subset U of |X| is called effective
if there is an effective morphism f: Y --> X such
that |f(Y)| = U. Since Y is uniquely
determined by U up to isomorphism, we often write U
for Y, and call U
an effective subobject of X;
f is called the effective morphism
of U.
More generally, a subset U of |X| is called
active if there is a morphism f:
Y --> X such
that |f(Y)|  U, and any morphism g: Z --> X
with |g(Z)|
U, and any morphism g: Z --> X
with |g(Z)|  U factors through f uniquely. The morphism
f is an active morphism, uniquely determined by U (but in
general |f(Y)|
U factors through f uniquely. The morphism
f is an active morphism, uniquely determined by U (but in
general |f(Y)| 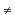 U), called the active morphism
of U. Any effective subset of |X| is active.
U), called the active morphism
of U. Any effective subset of |X| is active.
Remark 1.3.
An effective morphism plays the role of a local isomorphism in categorical
geometry. It has all the properties one would expect for a local isomorphism:
(a) An effective morphism is uniquely determined
by its image.
(b) An effective morphism is a monomorphism.
(c) An isomorphism is effective.
(d) A surjective effective morphism is an isomorphism.
(e) A composition of two effective morphisms is
effective.
(f) Suppose f: Y ®
X is an effective morphism. Then for any subset U  |Y|, U is
|Y|, U is
effective if and only if f(U) is effective,
in which case the induced morphism U --> f(U)
is an
isomorphism of effective subobjects (note that (a) -
(d) hold for any active morphism).
A metric presite C is effective
(resp. everywhere
effective) if any open subset (resp. any
subset) of any object is effective. Similarly a metric presite C
is called active
(resp. everywhere
active) if any open subset (resp. any subset) of any object
is active. A metric presite is locally
effective if open effective subsets of any object X form
a base for |X|.
Definition 1.4.
A metric site is a locally effective
metric presite satisfying the following condition:
If f: Y --> X
is a morphism in C and U an open effective subset of |X|,
then f-1(U)
is an open effective subset of |Y| (thus the
intersection of two open effective subsets of |X| is effective).
A metric pretopology t
on a category C is a metric
topology if (C, t)
is a metric site.
Example 1.4.1.
(a) The empty metric presite is a metric site.
(b) Any effective (resp. everywhere effective) metric
presite is a metric site, called an effective (resp.
everywhere effective) metric site.
(c) Since the empty subset  of any object X Î
C belongs to every base of |X|,
of any object X Î
C belongs to every base of |X|,  is effective if C is locally effective. Thus
any non-empty locally effective metric presite has at least
one empty object. This also implies that any initial object of a locally
effective metric presite (if exists) must be an empty
object.
is effective if C is locally effective. Thus
any non-empty locally effective metric presite has at least
one empty object. This also implies that any initial object of a locally
effective metric presite (if exists) must be an empty
object.
(d) Any locally effective metric presite with fibre products
is a metric site (this follows from (1.7b), and the
fact that, if f: Y --> X is a morphism and U
an open active subset of |X|, then f-1(U)
is active).
Suppose (C,  C)
and (D, C)
and (D,  D)
are metric presites. An isometry from C to D is a
functor D)
are metric presites. An isometry from C to D is a
functor  :
C --> D such that :
C --> D such that  D D is isomorphic to
is isomorphic to  C
(i.e., C
(i.e.,  D( D( (X))
is naturally homeomorphic to (X))
is naturally homeomorphic to  C(X)
for any X Î C),
and C(X)
for any X Î C),
and
 sends an
open effective morphism in C to an open effective morphism
in D. An isometry sends an
open effective morphism in C to an open effective morphism
in D. An isometry  is called an embedding (resp. equivalence) of metric presites if
the functor j is an embedding (resp. equivalence) of the underlying categories.
is called an embedding (resp. equivalence) of metric presites if
the functor j is an embedding (resp. equivalence) of the underlying categories.
Example 1.4.2.
Suppose (C,  C)
is a metric presite, B a subcategory of C. We define
the induced metric pretopology on B to be the restriction C)
is a metric presite, B a subcategory of C. We define
the induced metric pretopology on B to be the restriction  C|B
of C|B
of  on B. We say
(B, on B. We say
(B,  C|B)
(or simply B) is a subpresite of C if the inclusion functor
B ® C is an isometry of
metric presites from (B, C|B)
(or simply B) is a subpresite of C if the inclusion functor
B ® C is an isometry of
metric presites from (B,  C|B)
to (C, C|B)
to (C,  C). C).
Example 1.4.3.
Suppose (C,  C)
is a metric site. If a subpresite (B, C)
is a metric site. If a subpresite (B,  C|B)
of C is also a metric site, then we say that
B is a subsite of C. C|B)
of C is also a metric site, then we say that
B is a subsite of C.
Example 1.4.4.
Suppose (C,  ) is
a metric presite. For any object X Î
C denote by C/X the slice category
of objects f: Y ® X
over X. Let ) is
a metric presite. For any object X Î
C denote by C/X the slice category
of objects f: Y ® X
over X. Let  X:
C/X ® C be the functor
sending each f to Y. Then C/X
is a metric presite with the metric pretopology X:
C/X ® C be the functor
sending each f to Y. Then C/X
is a metric presite with the metric pretopology  C/X(f)
= |Y|, and C/X(f)
= |Y|, and  X
is an isometry from C/X to C. If C is a metric
site, then C/X is also a metric site. X
is an isometry from C/X to C. If C is a metric
site, then C/X is also a metric site.
Definition 1.5.
A strict
metric site is a metric site C in which the following
glueing lemma for morphisms holds:
Suppose X, Y are objects and {Ui}
is an open effective cover of |X|. Suppose for each
i we have a morphism fi: Ui
® Y such that the restrictions of
fi and fj to Ui
Ç Uj
are the same. Then there exists a unique morphism
f from X to Y such that the restriction of f
to Ui is fi.
Example 1.5.1.
Any full subsite of a strict metric site is a strict metric site.
Example 1.5.2.
The metric presite w(X)
of subspaces of a topological space X is an
everywhere effective, strict metric site. The metric presite W(X)
of open subsets of X is an effective, strict
subsite of w(X).
All the morphisms in w(X)
and W(X) are effective.
Let (C,  C)
be a metric presite. By a pointed object of C we mean a pair (X,
x) consisting of an object X Î
C and a point x Î
|X|. A morphism of pointed objects from (Y, y)
to (X, x) is a morphism f: Y ®
X such that f(y) = x. C)
be a metric presite. By a pointed object of C we mean a pair (X,
x) consisting of an object X Î
C and a point x Î
|X|. A morphism of pointed objects from (Y, y)
to (X, x) is a morphism f: Y ®
X such that f(y) = x.
Definition 1.6.
Suppose (C,  C)
is a metric presite and D a full subcategory of C. A
subset U of an object X Î
C is called D-exact if
the following conditions are satisfied: C)
is a metric presite and D a full subcategory of C. A
subset U of an object X Î
C is called D-exact if
the following conditions are satisfied:
(a) For any point x Î
U there is a morphism f: (Y, y) ®
(X, x) of pointed objects of C
such that Y Î
D and |f(Y)| Í
U.
(b) For any x Î
U the category D/(U, x) of pointed objects
f: (Y, y) ® (X,
x) over (X, x) such that Y
Î D and |f(Y)|
Í U is connected.
(c) A subset V of U is open in the subspace
U if for any morphism f: Y ®
X such that Y Î
D and |f(Y)| Í
U, f-1(V)
is an open subset of |Y|.
Suppose C is a metric presite. A subset U
of an object X Î
C is called exact if it is
a C-exact subset of |X|. A metric presite C
is called exact (resp. everywhere
exact) if any open subset (resp. any subset)
of any object X Î
C is exact.
Proposition 1.7.
Suppose C is a metric presite.
(a) A subset U of an object X is effective
if and only if U is active and exact (thus any
active, exact metric presite is an effective metric site).
(b) C is exact if the open exact subsets of any
object X form a base for |X| (thus any
locally effective metric presite is exact).
Proof. (a) One direction is obvious. Suppose U
is an active subset of X and f: Y ®
X is the active morphism of U. Suppose U
is exact. Then (1.6.a) means that |f(Y)|
= U, (1.6b) implies that |f| is injective,
and (1.6c) indicates that any subset V of U is open if f-1(V)
is open, so |f| is an embedding. Thus f is effective and
|f(Y)| = U is effective.
(b) Suppose open exact subsets of any object X
form a base for |X|. Let U be an open
subset of |X|. We verify the conditions of (1.6.)
for U:
First (1.6.a) follows from the fact
that U has an open exact cover {Vi} and (1.6a)
holds for each open exact subset Vi.
Suppose x Î
U. We have to prove that the category C/(U, x)
is connected. Let V be an open exact neighborhood
of x contained in U. Then C/(V, x) is a connected
subcategory of C/(U, x) (1.6b). It suffices
to prove that any object of C/(U, x) is connected
to an object of C/(V, x). Suppose f: (Y,
y) ® (X,
x) is an object of C/(U, x). Then
f-1(V)
is an open subset of Y containing y. Applying (1.6.a)
to an open exact subset of f-1(V)
containing y we can find a morphism g: (Z, z) ®
(Y, y) such that g(Z) Í
f-1(V).
Since fg: (Z, z) ®
(X, x) is an object of C/(V, x), we
see that the object f Î
C/(U, x) is connected to an object
fg Î C/(V,
x) by g. Suppose V is a subset of U such that
(1.6.c) holds for V. Take an open exact cover
{Vi} of U. Then (1.6.c)
holds for the subset V Ç
Vi of Vi for each i. Thus each
V Ç Vi
is open in Vi. Hence V is
open in U. n
Definition 1.8.
Suppose C is a category and D a full subcategory of C.
Suppose  D
is a pretopology on D. A pretopology D
is a pretopology on D. A pretopology  C
on C is called an extension of C
on C is called an extension of  D
on C if D
on C if  D
= D
=  C|D
and |X| is D-exact for any X C|D
and |X| is D-exact for any X  C.
C.
Remark 1.9.
It is easy to see that  C
is unique up to a natural isomorphism, if it exists.
We now show that such an extension C
is unique up to a natural isomorphism, if it exists.
We now show that such an extension  C
always exists: for any X Î
C consider the triples (Y, y,
f), where Y Î
D, y Î
|Y|, and f: Y ®
X is a morphism. Write (Y, y, f) ~ (Z,
z, g) if there is another triple (W,
w, h) with morphisms p: W ®
Y, q: W ®
Z, such that fp = h = gq,
p(w) = y and q(w) = z. Denote
by C
always exists: for any X Î
C consider the triples (Y, y,
f), where Y Î
D, y Î
|Y|, and f: Y ®
X is a morphism. Write (Y, y, f) ~ (Z,
z, g) if there is another triple (W,
w, h) with morphisms p: W ®
Y, q: W ®
Z, such that fp = h = gq,
p(w) = y and q(w) = z. Denote
by  C(X)
the set of equivalence classes of these C(X)
the set of equivalence classes of these
triples under the equivalence relation generated by ~.
Any morphism u: X ®
S in C induces a map  C(u): C(u):  C(X)
® C(X)
®  C(S)
sending each (Y, y, f) Î C(S)
sending each (Y, y, f) Î  C(Z)
to (Y, y, uf) Î C(Z)
to (Y, y, uf) Î  C(S).
If X Î D,
then C(S).
If X Î D,
then  C(X)
may be identified with the set C(X)
may be identified with the set  D(X).
A subset U of D(X).
A subset U of  C(X)
is open if for any Y Î
D and f: Y ®
X, f-1(U)
is an open subset of |Y|. These open subsets turns C(X)
is open if for any Y Î
D and f: Y ®
X, f-1(U)
is an open subset of |Y|. These open subsets turns  C(X)
into a topological spaces. If X Î
D, then C(X)
into a topological spaces. If X Î
D, then  C(X)
is naturally homeomorphic to the space C(X)
is naturally homeomorphic to the space  D(X).
Let D(X).
Let  C
be the pretopology on C defined by X ® C
be the pretopology on C defined by X ®  C(X)
for any X Î
C. Then we have C(X)
for any X Î
C. Then we have  D
= D
=
 C|D.
It is easy to verify that C|D.
It is easy to verify that  C(X)
is D-exact for any X Î
C. Thus C(X)
is D-exact for any X Î
C. Thus  C
is an extension of C
is an extension of  D
on C. D
on C.
Theorem 1.10.
Suppose (C,  C)
is a metric presite and D a full subcategory of C.
Suppose tC is
an extension of C)
is a metric presite and D a full subcategory of C.
Suppose tC is
an extension of  D
= D
=  C|D.
Then (C, C|D.
Then (C,  C)
is exact if and only if (D, C)
is exact if and only if (D,  D)
is exact. D)
is exact.
Proof. First suppose (D,  D)
is exact. We prove that the extension (C, D)
is exact. We prove that the extension (C,  C)
is exact. Let U be an open subset of
an object X of C. We show that U is C-exact
by verifying the conditions of (1.6). C)
is exact. Let U be an open subset of
an object X of C. We show that U is C-exact
by verifying the conditions of (1.6).
(a) Since |X| is D-exact, for any point
x Î U
there is a morphism f: (Y, y) ®
(X, x) such that Y Î
D (1.6a). Since D is exact, we can find a D-exact
open neighborhood V of y contained in
f-1(U).
Let g: (Z, z) ® (Y,
y) be a morphism with Z Î
D and |g(Z)| Í
V (1.6.a). Then fg:
(Z, z) ® (X, x)
is a morphism such that |fg(Z)| Í
U. This proves (1.6.a) for
U.
(b) Suppose x Î
U. Consider two pointed objects f: (Y, y) ®
(X, x) and g: (Z, z) ®
(X, x) over (X, x) in C/(U,
x). We have to prove that f and g are connected in
C/(U, x). We have seen in (a)
that any pointed object of C/(U, x) is connected to
a pointed object of D/(U, x).
Thus we may assume Y, X  D. Then f and g are connected in D/(|X|,
x) because |X| is D-exact. Using
the fact that D is exact we can easily verify that f and
g are connected in D/(U, x).
D. Then f and g are connected in D/(|X|,
x) because |X| is D-exact. Using
the fact that D is exact we can easily verify that f and
g are connected in D/(U, x).
(c) Suppose V is a subset of U such that
for any morphism f: Y ®
X with |f(Y)| Í
U, |f -1(V)|
is an open subset of |Y|. Suppose g: Z ®
X is any morphism with Z Î
D. For any h: W ®
Z with W Î
D and |h(W)| Í
g-1(U),
the subset (gh)-1(V)
= h-1(g-1(V))
is open because |gh(W)| Í
U. Since g-1(U)
is D-exact, this implies that g-1(V)
is an open subset of g-1(U),
thus an open subset of |Z|. Since |X| is D-exact, this means
that V is open in |X|, thus also open
in U. Conversely, suppose (C, tC) is exact.
Suppose U is an open subset of an object X
Î D. We show
that U is D-exact by verifying the conditions of (1.6).
(a') Since U is C-exact, for any point
x Î U
there is a morphism f: (Y, y) ®
(X, x) with f(Y) Í
U by (1.6.a). Since |Y| is D-exact,
we can find a morphism g: (Z, z) ®
(Y, y) with Z Î
D (1.6.a). Then fg: (Z, z)
® (X, x) is a morphism of
pointed objects of D such that |fg(Z)|
Í U. This
proves (1.6.a) for U.
(b') We prove that for any x Î
U, the category D/(U, x) is connected. Consider
two pointed objects f: (Y, y)
® (X, x) and g: (Z,
z) ® (X, x) over
(X, x) in D/(U, x). Since U is
C-exact, f and g are connected in C/(U,
x). Using the fact that  C
is an extension of C
is an extension of  D
we can show that f and g are also connected
in D/(U, x). D
we can show that f and g are also connected
in D/(U, x).
(c') Suppose V is a subset of U such that
for any morphism f: Y ®
X with |f(Y)| Í
U and Y Î
D, f-1(V)|
is an open subset of |Y|. Suppose g: Z ®
X is any morphism with g(Z) Í
U. For any morphism h: Y ®
Z with Y Î
D, we have |gh(Y)| Í
U. Thus (gh)-1(V)
= h-1(g-1(V))
is open. Since |Z| is D-exact, this implies that g-1(V)
is open. Since U is C-exact, this means
that V is open in U. n
Corollary 1.11.
Suppose (C,  C)
is a metric presite and D a full subcategory of C.
Suppose C)
is a metric presite and D a full subcategory of C.
Suppose  C
is an extension of C
is an extension of  D
= D
=  C|D.
Suppose (D, C|D.
Suppose (D,  D)
is exact and (C, D)
is exact and (C,  C)
is active. Then (C, C)
is active. Then (C,  C)
is an effective metric site, and (D, C)
is an effective metric site, and (D,  )
is a subsite of (C, )
is a subsite of (C,  C)
if D is dense in C. C)
if D is dense in C.
Proof. The first assertion follows from (1.10)
and (1.7.a). Now suppose D
is dense in C. Suppose f: Y ®
X is an open effective morphism in D; we prove that f
is effective in C. Since f is bicontinuous,
it suffices to prove that it is active in C. Suppose g: Z
® X is a morphism
in C such that |g(Z)| Í
|f(Y)|. Then for any morphism h: W ®
Z with W ” D, gh: W
® X has the image |gh(W)|
Í |f(Y)|.
Since f is effective in D, gh factors through f
uniquely. Since D is dense in C, this implies
that h factors through f uniquely, thus f is
active in C. This shows that D is a subsite
of C. n
Theorem 1.12.
Suppose (C,  C)
is a metric presite and D a full dense subcategory of
C. Suppose the glueing lemma (1.5) holds for
the morphisms from X to Y with X Î
D. Then (C, C)
is a metric presite and D a full dense subcategory of
C. Suppose the glueing lemma (1.5) holds for
the morphisms from X to Y with X Î
D. Then (C,  C)
is a strict metric site. C)
is a strict metric site.
Proof. We prove that C is strict by verifying
the condition of (1.5) for any objects X,
Y Î C
and an open effective cover {Ui} of |X|.
Suppose f, g Î
homC(X, Y) and f ¹
g. Since D is dense
in C, We can find Z Î
D and h: Z ®
X such that fh ¹ gh.
Since {h-1(Ui)}
forms an open cover of Z Î
D, by the glueing lemma we can find an open effective subset
V of |Z| contained in some h-1(Ui)
such that the restrictions of fh and gh to V are different
(because the collection of all such V forms an open
effective cover of |Z|). It follows that
the restrictions of f and g to Ui
are different. Now suppose for any i we have
a morphism fi: Ui ®
Y such that the restrictions of fi
and fj to Ui Ç
Uj are the same. For any object Z Î
D and any morphism h: Z ®
X, let
{Vj}be an effective open cover of |Z|
such that h(Vj) Í
Ui for some Ui. Denote by hi
the restriction of h to Vi.
Then fihi and fjhj
agree on Vi Ç
Vj. By the glueing lemma for morphisms
from Z to Y these fihi determine
a morphism h': Z ®
Y. We obtain a map homC(Z,
X) ® homC(Z,
Y) given by h ®
h' for each Z Î
D. Since D is dense in C, the collection
of all these maps determines a morphism f Î
homC(X, Y) whose restriction to
each Ui is fi.
The uniqueness of f is obvious. This proves that (C,  C)
is strict. n C)
is strict. n
[Next Section][Content][References][Notations][Home]
|