|
6. Algebras
If A and B are sets, the Cartesian
product A B of
A
and B is defined as the set of all ordered pairs (a,
b),
with a A and bB.
In symbols,
A B = {(a,
b)
| a A and
b B}.
In general, if A0, ..., An-1 are sets,
then we set
A0A1
... An-1
= {(a0, a1, ..., an-1)
| a0 A0,
a1
A1, ..., an-1
An-1}.
If A0 = ... An-1 = A, then we set
An = A0 ... An-1,
called the n-fold direct power ofA.
Thus An is the set of all n-tuples of elements
of A. We denote A0 to be { }.
If f: A --> B is a mapping of two sets we write
fn
for the induced mapping
An --> Bn
sending (a1, ..., an) to (f(a1),
..., f(an)).
Definition 6.1. (a) An operation of
rank n (or n-ary operation)
on A is a function
An
into
A.
(b) A (finitary) operation
on A is an operation of rank
n on A for some natural
number n.
Remark 6.2. (a) Operations of rank 0 on a nonempty set
are functions that have only one value, called constants,
which are identified with their unique values.
(b) Operations of rank 1 on A are unary
operations, which are functions from A into A.
(c) Binary and ternary
operations are operations of rank 2 and
3 respectively.
Denote by A(n) the set of operations of rank n
on A.
Definition 6.3. A type of algebra is
a set  with a map
a:
--> N, where N is the set of natural numbers;
the elements of are called
operators,
and if  ,
then a() is called
the arity of .
If a() = n we
also say that is n-ary,
and we write
(n) = {
| a() = n}.
Definition 6.4. Let A be a set and
an operator domain; then an -algebra
structure F on A is a family of mappings
F(n): (n)
--> A(n).
For simplicity we shall identify any n-ary operator
with the the associated operation F(n)()
of rank of n on A, called a basic
operation of .
Definition 6.5. A set A together with an -algebra
structure F is called an -algebra.
Given an -algebra A
and (n),
then applied to an n-tuple
(a1, ..., an) from A given an
element of A which we write as (
a1a2...an).
Example 6.5.1. If A has only one element, there
is only one way of defining an -algebraic
structure, because for any integer n, there is only one mapping
from An to A. An -algebra
with only one element is called trivial;
all trivial algebras are isomorphic.
In the following we fix a type of algebra
and consider -algebras.
Definition 6.6. Given -algebras
A
and B, a mapping f: A --> B, and (n),
we say the f is compatible with
if
fn
= f.
We say f is a homomorphism fromAtoB
if it is compatible with any basic operation of .
Clearly composites of homomorphisms are homomorphisms. Thus the class of -algebras
with all the homomorphisms between them form a category, which we shall
denote by ().
Definition 6.7. Consider an -algebra
A.
(a) A subset B of A is called closedwith
respective to an operation
of rank
n
if
sends the elements of Bn into Bn.
(b) A subset B of A is called a subalgebra
of
A if it is closed with respective to any basic operations in ..
Remark 6.8. (a) Any subalgebra B of an -algebra
A
is itself an -algebra
with the basic operations
induced from the basic operations of
such that the inclusion mapping B --> A is a homomorphism
of -algebras..
(b) Any intersection of subalgebras is a subalgebra.
(c) The intersection B of subalgebras containing a subset S
of
A is called the subalgebra generated
by S, and S is the generating set of B.If
the subalgebra generated by S is A then we say that
S
is a generating set of A.
Lemma 6.9. Let A be an -algebra
and X a generating set of A. Then any homomorphism of A
into another -algebra
is completely determined by its restriction to X.
Proof. If t and s are two homomorphisms from A
to B which agree on X, the subset A' of all the elements
of A at which t and s agree is a subalgebra which
contains X. Since X generates A, we have A
= A'.
Let X be a set whose elements are called variables.
Let be a type of algebras.
The set T(X) of terms of type
over X is the smallest set such that
(i) X 0
T(X).
(ii) If p1, . . . , pn
T(X) and f n
then the "string" f(p1,...,pn) T(X).
For p T(X)
we often write p as p(x1,,...,xn)
to indicate that the variables occuring in p are among x1,...,xn.
A term p is n-ary if
the number of variables appearing explicity in p is  n.
Given a term p(x1,...,xn) of type
over some set X and given an algebra A of type
we define a mapping pA: An --> A
as follows:
(1) if p is a vairable xi, then
pA(a1,...,an) =
ai
for ai,...,anA,
i.e., p is the i-th projection map;
(2) if p is of the form  (p1(x1,...,xn),...,pk(x1,...,xn)),
where k,
then
pA(a1,...,an) = A(p1(a1,...,am),...,pk(a1,...,an)).
In particular if p =
then pA = A.
pA is the term function
on A corresponding to the term p (Often we will drop the
superscript A).
Given and X,
if T(X)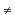 
then T(X) is an algebra of type 
whose fundamenstal operations satisffies
T(X)(p1,...,pn)
= (p1,...,
pn)
for n
and pi T(X),
1
i n. (T()
exists iff 0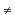
).
T(X) is called the term agebra
of type over
X.
Proposition 6.10. (a) T(X) is a free object of
() over X.
(b) () is an exact algebraic
category.
Proof. (a) Consider any mapping f: X -->
A from X to an -algebra
A. Then f extends to a mapping f': T(X)
--> A sending each term p(x1,...,xn)
to pA(f(x1),...,f(xn)),
which is an -algebra homomorphism,
and f' is unique as X generates T(X).
(b)
[References][Notations][Home]
|